티스토리 뷰
KL Divergence는 서로 다른 두 확률 분포간의 차이를 계산하기 위해 사용된다.
서로 다른 두 분포 P와 Q에 대해서 KL Divergence는 다음과 같은 식으로 계산된다.

그렇다면, 왜 이러한 식을 사용해서 두 분포간의 차이를 계산할 수 있다는 것일까?

먼저 우리가 차이를 구하고자 하는 두 분포를 정의해보자.
True Coin의 분포가 P 분포이고 Coin2의 분포가 Q 분포이다.

우리가 어떤 코인으로 던졌는지 모르고 있는 상태로, 동전의 앞/뒷면이 나온 결과가 주어졌다고 가정하자.
이러한 결과가 주어졌을 때,
1) True Coin일 경우 우리가 얻은 결과가 나올 확률, 2) Coin2일 경우 우리가 얻은 결과가 나올 확률
을 조건부 확률을 이용해서 계산할 수 있다.
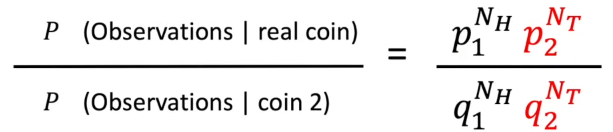
(위 식에서 앞면이 나온 횟수가 NH, 뒷면이 나온 휫수가 NT가 된다.)
각 동전에서 얻은 조건부 확률을 각각 분모와 분자로 하여, 하나의 유사도를 측정할 수 있다.
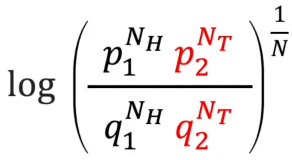
위 식에서 정규화를 위해 지수에 1/N (전체 동전을 던진 횟수)를 취해주고 log를 취해준다.
그리고 이 식을 log의 성질을 이용해서 간단히 전개하면,

위 식과 같은 결과가 나온다. 만일 우리가 동전을 수없이 많이 던진다면, NH / N은 True Coin을 던졌을 때, 앞면이 나올 확률 p1에 수렴할 것이다. 같은 원리로, NT / N은 p2에 수렴할 것이다. 이를 반영하여 식을 새로 쓰면,

가 되고 이식을 다시 정리하면,

가 되어 우리가 알고 있는 KL Divergence의 식으로 정리할 수 있다.
즉 KL Divergence는

을 통해서 두 분포간의 차이를 구하고 있던 것이다.
출처 :
Intuitively Understanding the KL Divergence
'수학' 카테고리의 다른 글
| 이산 확률 분포 정리 (0) | 2021.06.19 |
|---|---|
| 조건부확률과 베이즈 정리 (0) | 2021.06.14 |
- Total
- Today
- Yesterday
- #information_retrieval
- #1405번
- javascript
- #BOJ #2467번 #투포인터알고리즘
- #BOJ #알고리즘 #1034번
- directives
- LeetCode
- sliding window
- LLM
- 베르누이분포
- #BOJ #그리디알고리즘
- two-pointers
- 조건부확률
- NAACL21
- PyTorch
- Rag
- #브루트포스
- emnlp
- GCN
- KL_Divergence
- CoT
- python
- emnlp2024
- DECI
- 파이토치
- iclr
- #BOJ
- 인과관계추론
- #BOJ #유클리드호제법
- llm agent
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
