티스토리 뷰
이산 확률 분포란?
확률 변수가 가질 수 있는 값이 연속적이지 않고 구분 되는 경우
예를 들어 주사위를 한번 던져 나오는 수를 확률변수 X라고 하면, X는 1, ,2, 3, 4, 5, 6 중 하나인 수이다.
즉, X는 이산 확률 분포인 확률 변수라고 할 수 있다.
이와 달리 임의로 뽑은 학생의 키를 확률변수 Y라고 하면 Y는 연속적인 값을 가지므로 Y는 연속 확률 분포인 확률 변수이다.
(엄밀히 말하자면 확률변수가 나올 수 있는 값의 수가 가산적인 경우(countable) 이산확률분포라고한다.)
확률 질량 함수(Probability Mass Function, PMF)
이산 확률 분포에서 확률 변수의 어떤 값이 등장할 확률을 나타내는 함수이다.
다시 한번 주사위를 예로 들자면, 주사위를 한번 던저 나오는 수를 확률 변수 X라고 하면
각각의 눈이 나올 확률은 같으므로 아래와 같이 나타낼 수 있다.
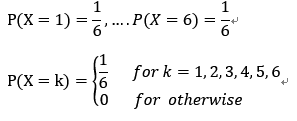
여러가지 이산 확률 분포
1. 베르누이 분포
어떤 실험의 시행 결과가 0 또는 1 두가지 만 나오는 경우의 확률 분포
동전을 던졌을 때 확률변수 X를 앞면이 나오면 0, 뒷면이 나오면 1이라고 하면 X는 베르누이 분포를 따른다.
뒷면이 나올 확률(확률 변수가 1일 확률)을 p라고 하면 X~Bernoulli(p)라고 쓸 수 있으며,
확률 질량함수는 아래와 같고 평균 E[X]=p, 분산 Var[X]=p(1-p)이다.

2. 이항 분포
위의 베르누이 분포를 n번 시행했을 때 확률 분포
동전을 n번 던졌을 때 확률변수 X를 동전이 뒷면이 나온 횟수라고 하면, X는 이항 분포를 따른다.
뒷면이 나올 확률(확률 변수가 1일 확률)을 p라고 하면 X~Binomial(n, p)라고 쓸 수 있으며,
확률 질량함수는 아래와 같고 평균 E[X]=np, 분산 Var[X]=np(1-p)이다.

확률 밀도 함수를 자세히 보면, (n번 던져 동전의 뒷면이 k번 나오는 경우의 수)*(n번 던져 동전의 뒷면이 k번 나오는 확률)임을 알 수 있다.
'수학' 카테고리의 다른 글
| KL Divergence 유도 과정 진짜 쉽게 알아보기 (1) | 2022.11.21 |
|---|---|
| 조건부확률과 베이즈 정리 (0) | 2021.06.14 |
- Total
- Today
- Yesterday
- python
- iclr
- NAACL21
- javascript
- emnlp2024
- LeetCode
- #1405번
- #브루트포스
- #BOJ
- llm agent
- PyTorch
- two-pointers
- directives
- #BOJ #2467번 #투포인터알고리즘
- #BOJ #유클리드호제법
- 조건부확률
- 베르누이분포
- KL_Divergence
- #information_retrieval
- 인과관계추론
- emnlp
- #BOJ #알고리즘 #1034번
- LLM
- GCN
- 파이토치
- Rag
- #BOJ #그리디알고리즘
- CoT
- sliding window
- DECI
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
